Measuring the association between sites and centuriation grid

Why measure association?

• Dwelling sites in the northern Ager Cosanus (centuriation of Cosa, Italy) dated to the 2nd century BC, which have been found "only on the major axes of the centuriation" (Attolini, et al.1990:145) - for convenience of access?
• Roman tombs, by law, when the limites were public roads. For example the Lex Sempronia says sepulchra extremis finibus circa decumanos et kardines, qui vicem itineris publici teneant, collocantur.
• Post-roman sites of religious significance, such as mosques near Damascus, three of which line up along a kardo , now hardly visible (Dodinet et al 1990). Continuity of specific ritual sites? Convenience?
• Modern features in north Africa, since Caillemer and Chevallier (1954: 458) tell us "Des routes, des voies ferrées, des pistes d'aérodrome, des limites de commune s'orientent de même pour éviter de couper les cultures dont les contours correspondent toujours à la répartition antique du sol; il arrivent souvent que de grandes fermes modernes soient situées à l'emplacement de ruines romaines, dans l'angle de centuries." These features appear to be located, in the main, for pragmatic reasons.

Whatever the reason, we expect that within the area of a centuriation the distribution of sites of many different types will not be random. So we can test a cadastral hypothesis by examining the distribution of distances of sites from the grid lines, when compared to the distribution which we would see if the points fell by chance.

Earlier statistical tests of spatial distribution

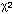• Hodder and Orton (1976:226-229) counted the numbers of late Iron Age inscribed coins found in three bands covering arbitrary distances from Roman roads in central and southern England, and compared them with the relative areas within the bands. They used both the (chi squared) and Kolmogorov-Smirnov tests to demonstrate a significant bias towards the roads. In the latter test, since they had divided the total area in three, they were obliged to interpolate the curve for expected distances from just three points.

  Given that GIS systems are now more widely available, this is now unnecessary. For example, the IDRISI distance function can be used to obtain an almost continuous distribution of cell distances from the roads. This can then be compared to the distances of the coins, with a more accurate (and more statistically significant) result (Kvamme 1992:79).

• Reilly (1988:180-186) was facing a similar problem, but he chose to generate the distribution of distances of points scattered at random by monte-carlo simulation, rather than measure bands of area. He did this in order to evaluate Goodier's (1983:1984) method for measuring boundary association.

  Goodier had used empirical data which suggested that for irregular boundaries the boundary length would be less than one sixth of the square root of the area. She then used a formula to calculate the area of bands of constant width along the boundary. Reilly showed that this method is flawed. For irregular boundaries it is much more reliable to use the actual boundaries of the system being studied.

A tests of site distribution in a centuriation

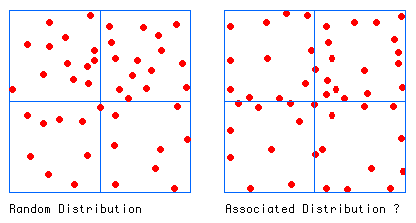
To understand what we are trying to do, consider the distributions of sites (red blobs) with respect to limites (blue lines) in the figure above. How can we tell a random distribution (left) from a distribution which does not look random (right)?

The Kolmogorov-Smirnov single sample test can be conveniently used. In general, if we have observations taken at a sequence of times or distances, the test compares the actual number of observations (up to that time or distance) with the number that would have been seen by chance (the nul hypothesis). For most of the observations there is a difference between these two. The largest value of this difference (positive or negative) is D, the Kolmogorov-Smirnov statistic. It tells us how likely it is that the actual distribution of observations would be seen if the nul hypothesis were true. Naturally, for a given level of significance the critical D value depends on the number of observations. The less numerous they are, the higher the critical values.

If points are scattered uniform randomly in a square grid, then the number of points which we expect to see at a given distance d from the sides is proportional to the area containing points at less than that distance, compared to the whole area. By symmetry, we can consider a quarter of the square, as in the figure below. The expression for the area of the yellow band is then also the expression for the distribution of points on the nul hypothesis of uniform random distribution.

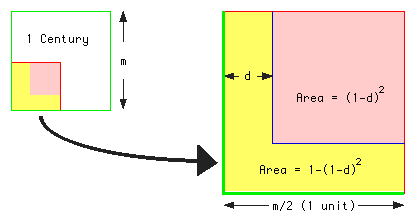
For example, for d = 0.5 we have the expectation that 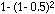, 75%, of points scattered at random in any grid square will fall within the band so defined, i.e. at distances up to a quarter (0.5 x 1/2) grid distance from a grid line. Again, it is certain that any point will fall within half the grid distance, since the formula gives the expectation for this distance as 1 (or 100%).

Suppose that we have n points arranged in increasing order of distance from the nearest edge of the square in which it lies (the nearest limes ). For the 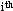point, the number of observations made (up to that point) is i/n.

The test statistic (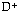, see below) is thus the maximum value of....

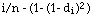
where 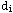is the distance of the 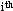point.

In this case, since only an association with limites has theoretical significance, we are only interested in positive values of D (that is 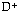). Such a positive value would indicate that more points have been observed (within a given distance of the grid lines) than we would expect by chance.

Tables of critical values of 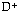show with what confidence we can reject the null hypothesis. One such table, giving values for sample sizes up to 100 was first presented by Miller (1956). For larger samples the critical value, 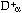, for a given probability,, can be calculated using a version of the asymptotic formula given by Miller, which was originally due to Smirnov:

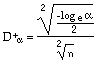
We can calculate values of the numerator of this expression for commonly used significance levels

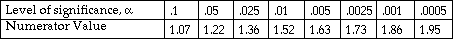
Each numerator value divided by the square root of the sample size gives the critical value of 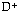. So, for example, if we have 400 observations (square root = 20) the critical value for the .005 significance level is .082. If the D value for the observations achieves this then we can say that the observed distribution would have occurred with less than 0.5% probability on the basis of the nul hypothesis.

Implementation

References

Attolini, I., Cambi, F., Castagna, M., Celuzza, M., Fentress, E., Perkins, P., and Regoli, E. 1990. Political geography and productive geography between the valleys of the Albegna and the Fiora in northern Etruria. In Roman Landscapes: Field Survey in the Mediterranean. edited by Barker, G. and Lloyd, J. pp. 142-151. British School at Rome, Rome.

Caillemer, A., and Chevallier, R. 1954. Atlas des centuriations de Tunisie. IGN, Paris.

Dodinet, M., Leblanc, J., and Vallat, J.-P. 1987. Utilisation de moyens informatiques en archéologie du paysage. Dialogues d'histoire ancienne 13 : 315-355.

Goodier, A. J. 1983. The Formation of Boundaries in the Anglo-Saxon Period: A Statistical Study. In Computer Applications and Quantitative Methods in Archaeology. edited by Haigh, J. G. B. pp. 93-101. School of Archaeological Sciences, Bradford.

Goodier, A. J. 1984. The Formation of Boundaries in the Anglo-Saxon Period: A Statistical Study. Medieval Archaeology 28 : 1-21.

Hodder, I., and Orton, C. 1976. Spatial Analysis in Archaeology. Cambridge University Press, Cambridge.

Kvamme, K. L. 1992. Geographic Information Systems and archaeology. In CAA91: Computer Applications and Quantitative Methods in Archaeology 1991. BAR International Series S577. edited by Lock, G. and Moffett, J. pp. 77-84. Tempus Reparatum, Oxford.

Miller, L. H. 1956. Table of Percentage Points of Kolmogorov Statistics. Journal of the American Statistical Association 51 : 111-121.

Reilly, P. 1988. Computer Analysis of an Archaeological Landscape. BAR 190. British Archaeological Reports, Oxford.

(e-mail j.peterson@uea.ac.uk)